この記事はStan Advent Calender 2018の17日目の投稿です。bayesplotにtidybayes,brmsパッケージなど,今年も盛り上がっておりますが,この記事では今年もやはりニッチなところを攻めたいと思います。なお,この記事の内容はMatti Vuorre氏のブログを大いに参考にしています。
多段階評定データの信号検出モデル
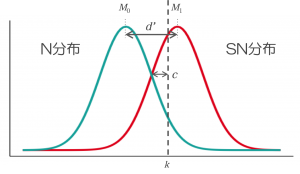
信号検出モデルは通常,「学習した/学習していない」(再認課題)や「単語/非単語」(語彙判断課題)といった,実験参加者に2値の反応を求める課題において,参加者の2種の刺激の弁別力と反応バイアスを求めるために用いられます。このとき,2種の刺激強度の分布と判断基準k,弁別力d,反応バイアスcの関係は以下のようになります。
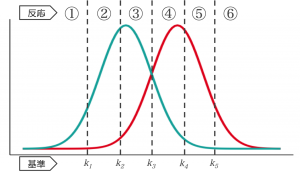
しかしながら,反応時の確信度に基づいて,参加者に3段階以上の反応を求めることもできます。例えば再認課題において,「①:絶対に学習していない,②:おそらく学習していない…⑥:絶対に学習した」の6段階で反応するよう求めるような場合です。このとき,非学習項目と学習項目の刺激強度の分布に対して,5つの判断基準※1が設けられることになります。
数式的な部分はさておき,こうした複数の判断基準をおく信号検出モデルは,順序を伴うカテゴリカルデータの分析に用いられる順序プロビットモデル(Ordered Probit Model)と等価であり (Vuorre, 2017)※2,順序カテゴリカルデータを目的変数とした回帰モデルとして表現できます。ベイズでStanを使った回帰モデル,とくれば,昨日のStanアドカレ記事でも紹介されていたbrmsパッケージの出番です。
brmsパッケージを用いた等分散信号検出モデル
データとして,MPTinRパッケージに含まれる”roc6”というサンプルデータを使用します。6段階での再認課題を行なった複数の研究のデータがまとめられたもので,左6列はold項目(学習した項目)のデータであり,old項目のうち高い確信度でnew(学習していない)と回答されたもの(“OLD_3new”),中程度の確信度でnewと回答されたもの(“OLD_2new”)…高い確信度でoldと回答されたもの(“OLD_3old”)という順番で並んでいます。続く6列がnew項目に対する反応です。びっくりするほどtidyでないデータですね。
#パッケージ読み込み library(tidyverse) library(brms) library(MPTinR)
#データ読み込み dat <- roc6 head(dat)
> head(roc6) OLD_3new OLD_2new OLD_1new OLD_1old OLD_2old OLD_3old NEW_3new NEW_2new NEW_1new NEW_1old NEW_2old NEW_3old exp id 24 6 8 3 2 6 175 101 77 5 3 9 5 Dube_2012-P 1:Dube_2012-P 25 3 4 1 0 11 181 174 12 10 3 1 0 Dube_2012-P 2:Dube_2012-P 26 15 10 1 0 22 152 143 50 0 0 6 1 Dube_2012-P 3:Dube_2012-P 27 50 4 3 1 2 140 180 8 5 0 2 5 Dube_2012-P 4:Dube_2012-P 28 5 3 3 0 4 185 190 3 3 2 1 1 Dube_2012-P 5:Dube_2012-P 29 10 32 16 17 32 93 54 81 26 13 18 8 Dube_2012-P 6:Dube_2012-P
このデータから,Dube(2012)※3のPicture条件とWord条件のデータを抽出して使用したいと思います。目的変数が1(“3new”)〜6(“3old”)の反応カテゴリ,説明変数がold項目かnew項目かを表す2値の変数となるようにデータを整形します (煩雑な処理ですので,必要な方だけご覧ください)。
#Dube(2012)のデータを抜き出して整形
dat_P <- roc6 %>%
filter(exp == "Dube_2012-P") %>%
select(-exp) %>%
separate(id, c("id", "exp"), sep=":") %>%
select(-exp) %>%
gather(key, count, -id) %>%
separate(key, into = c("isold", "response")) %>%
mutate(isold = ifelse(isold=="OLD", 1, 0)) %>%
mutate(y = as.integer(substr(response, 1, 1)),
yy = substr(response, 2, 4),
yy = ifelse(yy=="old", 1, -1),
y = y*yy,
y = ifelse(y < 0, y+4, y+3)) %>%
select(-yy) %>%
mutate(id = as.integer(id))
dat_P <- dat_P[rep(seq_len(nrow(dat_P)), dat_P$count), c("id", "isold", "y")]
dat_P <- arrange(dat_P, isold, y)
dat_W <- roc6 %>%
filter(exp == "Dube_2012-W") %>%
select(-exp) %>%
separate(id, c("id", "exp"), sep=":") %>%
select(-exp) %>%
gather(key, count, -id) %>%
separate(key, into = c("isold", "response")) %>%
mutate(isold = ifelse(isold=="OLD", 1, 0)) %>%
mutate(y = as.integer(substr(response, 1, 1)),
yy = substr(response, 2, 4),
yy = ifelse(yy=="old", 1, -1),
y = y*yy,
y = ifelse(y < 0, y+4, y+3)) %>%
select(-yy) %>%
mutate(id = as.integer(id))
dat_W <- dat_W[rep(seq_len(nrow(dat_W)), dat_W$count), c("id", "isold", "y")]
dat_W <- arrange(dat_W, isold, y)
整形後のデータは以下のようになります。”isold”は項目がold項目かどうかを表す2値の変数です。”y”は参加者の1〜6の反応カテゴリを表します。
> head(dat_P) id isold y 1 1 0 1 2 1 0 1 3 1 0 1 4 1 0 1 5 1 0 1 6 1 0 1 > head(dat_W) id isold y 1 1 0 1 2 1 0 1 3 1 0 1 4 1 0 1 5 1 0 1 6 1 0 1
brmsパッケージのbrm関数を使って順序プロビットモデルを当てはめます。
#順序プロビットモデルの当てはめ
fit_P <- brm(y ~ isold,
family = cumulative(link="probit"),
data = dat_P,
iter = 2000,
warmup = 1000,
chain = 4)
fit_W <- brm(y ~ isold,
family = cumulative(link="probit"),
data = dat_W,
iter = 2000,
warmup = 1000,
chain = 4)
summary(fit_P)
summary(fit_W)
> summary(fit_P)
Family: cumulative
Links: mu = probit; disc = identity
Formula: y ~ isold
Data: dat_P (Number of observations: 10800)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept[1] 0.53 0.02 0.50 0.57 6012 1.00
Intercept[2] 1.17 0.02 1.13 1.21 5853 1.00
Intercept[3] 1.31 0.02 1.27 1.35 5793 1.00
Intercept[4] 1.39 0.02 1.35 1.43 5665 1.00
Intercept[5] 1.68 0.02 1.63 1.72 5147 1.00
isold 2.21 0.03 2.16 2.26 5020 1.00
Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
is a crude measure of effective sample size, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
> summary(fit_W)
Family: cumulative
Links: mu = probit; disc = identity
Formula: y ~ isold
Data: dat_W (Number of observations: 8800)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept[1] -0.56 0.02 -0.60 -0.53 4217 1.00
Intercept[2] 0.19 0.02 0.16 0.23 5223 1.00
Intercept[3] 0.48 0.02 0.45 0.52 5257 1.00
Intercept[4] 0.62 0.02 0.59 0.66 5245 1.00
Intercept[5] 1.02 0.02 0.98 1.06 4883 1.00
isold 0.90 0.02 0.86 0.95 4637 1.00
Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
is a crude measure of effective sample size, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
それぞれ,intercept[1]〜[5]が参加者の反応カテゴリを分ける基準,isoldが弁別力d’の推定値です。Picture条件と比べるとWord条件では学習項目と非学習項目の区別がつきにくく,弁別力も低い,という結論になりそうです。
反応が2値から多段階になることで,信号検出モデルはさらに汎用性の高い認知モデルになるように思います。信号検出モデルのような古典的な認知モデルは,パラメータの解釈に一定のコンセンサスがあることがメリットだと感じています。brmsパッケージの登場でStanを使ったモデリングへの敷居も下がりつつある今,色々な領域のデータにこれらの認知モデルを当てはめることで,何らか楽しいことが言えるといいのかな,と思います。
Enjoy!
(本当はこの後,不等分散の信号検出モデルとかbayesplotで図示とかしたかったのですが,時間切れのためここまでとします。また余裕があれば追記するかも…されないかも…)
※1 Fig.2では判断基準をk1〜k5としていますが,基準(criteria)ということでc1〜c5で表すことが多いようです。Fig.1の反応バイアスcとの混同を避けるため,ここでは添字kを使っています。
※2 Bayesian Estimation of Signal Detection Models, Part 3 https://vuorre.netlify.com/post/2017/10/16/bayesian-estimation-of-signal-detection-theory-models-part-3/
※3 Dube, C., & Rotello, C. M. (2012). Binary ROCs in perception and recognition memory are curved. Journal of Experimental Psychology: Learning, Memory, and Cognition, 38(1), 130.