この記事はJASP Advent Calendar 2021の7日目の記事です。
ほぼアドベントカレンダー専用と化しているこのブログですが,今年は統計ソフトJASPのアドカレに参加させていただくことにしました。というのも,JASPのオンラインテキストである「JASPで統計を学ぼう!」のChapter 13の翻訳を担当しているからです。
Chapter 13では,多元配置の分散分析(ANOVA)および共分散分析(ANCOVA)について,概念的説明とJASPによる分析例の紹介が行われています。しかしながら,JASPの強みであるベイジアン分析についてはChapter 14で少し触れられているのみです。
そこでこの記事では,JASPでのANOVAとANCOVA,およびベイジアンANOVAとANCOVAについて実行例を示しながら見ていこうと思います。なお,以下の分析はすべて,Windows版のJASP ver 0.16上で実行しています。
JASPによる分散分析
まずはおなじみの分散分析を実行してみましょう。データセットはJASPのライブラリにある”Beer Googles”データを使用します。”開く”→”データ ライブラリ”→”3. ANOVA”からデータを開いてみましょう。
すでに結果が出力されている…だと…? (サンプルデータを使った場合の仕様のようです)
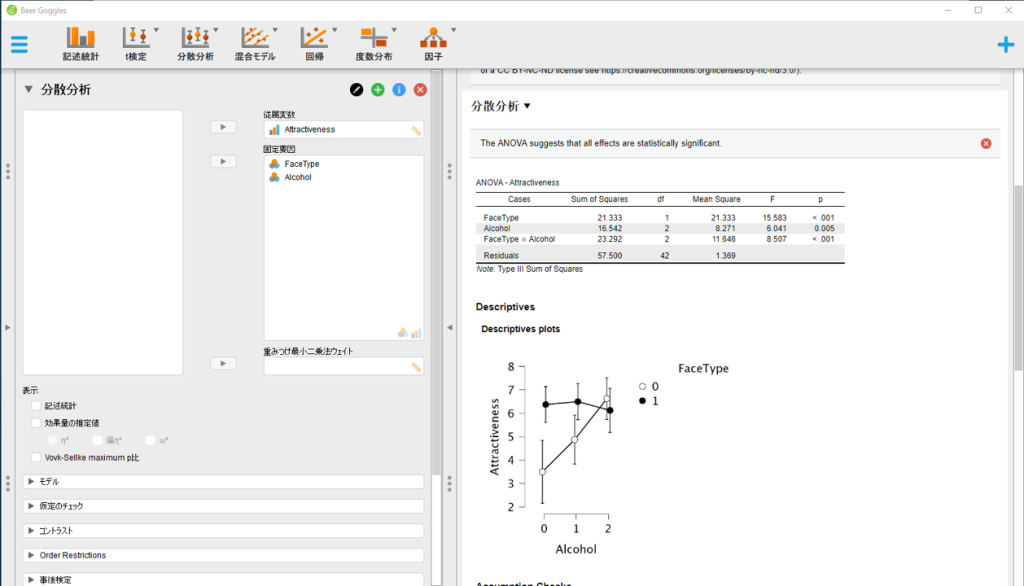
説明が前後しましたが,”Beer Googles”データセットには顔の種類(FaceType: 0=魅力的でない/1=魅力的)と飲酒量(Alcohol:0= プラセボ/1=弱飲酒/2=強飲酒),および魅力度(Attractiveness: 10件法で評定)の3つのデータが含まれています。顔の種類と飲酒量という2つの要因に応じて,魅力度の評定値が変わるのかどうかを,顔の種類2水準×飲酒量3水準の参加者間要因の分散分析で検討することができます。”従属変数”ボックスに魅力度の変数を,”固定要因”ボックスに顔の種類と飲酒量の変数を投入します。記述統計量や効果量を算出するオプションもありますね。
出力された分散分析表から,顔の種類の主効果,飲酒量の主効果,顔の種類と飲酒量の交互作用のいずれもp < .05で有意であることが分かります。
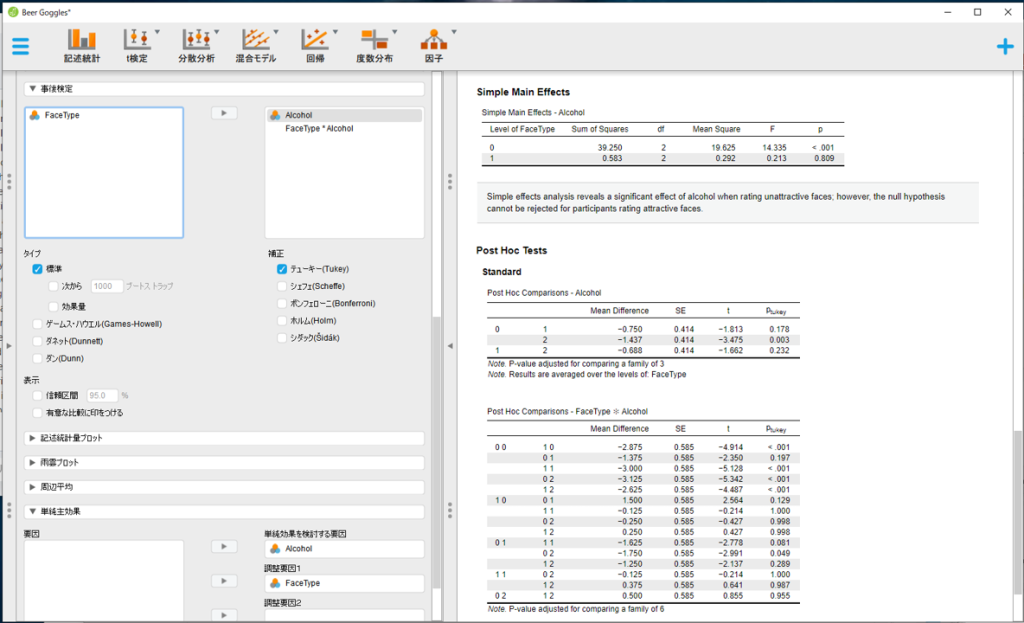
単純主効果の検定や事後検定は,左画面のメニューから行えます。
いずれも,見たい主効果や交互作用をボックスに投入するだけです。事後検定の出力は少々煩雑ですが,2桁の数字の各位が各要因の水準に対応しています。例えば,顔の種類0,飲酒量0の条件と顔の種類1,飲酒量0の条件に有意差があるかどうかを確かめたければ,”00″-”10″の行を確認すればOKです。顔の種類0,飲酒量2の条件と顔の種類1,飲酒量2の条件の比較は”02″-”12″の行です。これらの結果から,「飲酒していない条件(プラセボ条件)では魅力的な顔の方が魅力度の評定値が高いが,飲酒した条件では2つの顔の魅力度に差がなくなる」という結論になりそうです。やったね(?)
JASPによるベイジアンANOVA
同じデータセットについて,ベイジアンANOVAも実行してみましょう。上部の”分散分析”のメニューから,”ベイジアン”のグループ内の分散分析を選択します。先ほどと同様,”従属変数”と”固定要因”のボックスにそれぞれの変数を投入します。
従来の分散分析の結果を見慣れている方は,分散分析表が出力されないので,少々面食らうかもしれません。というのも,JASPのベイジアン分散分析は,”分散分析”という名前こそ付いていますが,従来の(頻度主義統計学の)分散分析とは異なり,平方和の分解や平均平方に基づくF値の算出などは行いません。同じ分散分析という名前がついていますが,内部で行っている計算は別物であるということを意識しておいた方が良いでしょう(そもそも有意性検定とベイズ推定が別々の枠組みなのですが)。
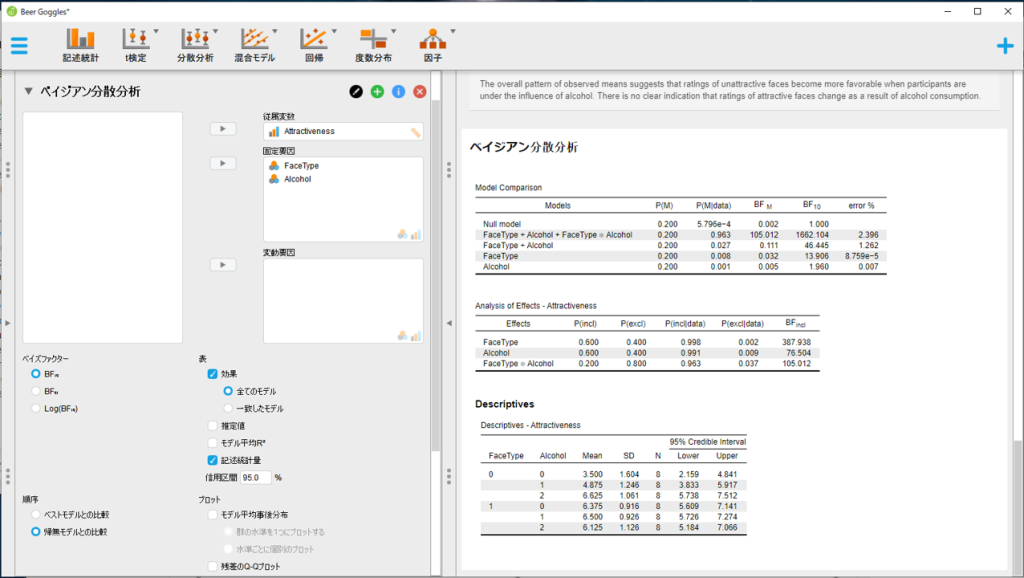
ベイジアン分散分析では,対立仮説や帰無仮説を含む複数のモデルの比較を行います。”Model Comparison”の表の”Models”列に,今回の2要因分散分析において想定し得るすべてのモデルが示されています。「FaceType + Alcohol + FaceType * Alcohol」は,「顔の種類の主効果,飲酒量の主効果,顔の種類と飲酒量の交互作用のすべてを含む」モデルという意味です。「FaceType + Alcohol 」は,「顔の種類の主効果と飲酒量の主効果を含む」モデル(=交互作用のないモデル)という意味になります。一番上の「Null model」は,いずれの項も含まないモデルであり,帰無仮説に相当します。
これらのモデルを比較する際には,BF(ベイズファクター)という値が重要になります。”順序”のオプションを”帰無モデルとの比較”にしておくことで,BF10列に示された値を「帰無仮説と比較してそのモデルが何倍確からしいか」と解釈することができます。BFの基準としてはKass(1995)の基準などが提案されており,今回の結果では2つの要因の主効果および交互作用をすべて含むモデルがもっとも支持されたといえます(BFの判断基準についてはChapter 14もご参照ください)。”効果”のオプションをオンにすることで,それぞれの主効果と交互作用のBFを比較することもできます。BFinclの値から,2つの要因の主効果,および交互作用はいずれも十分に大きいといえそうです。
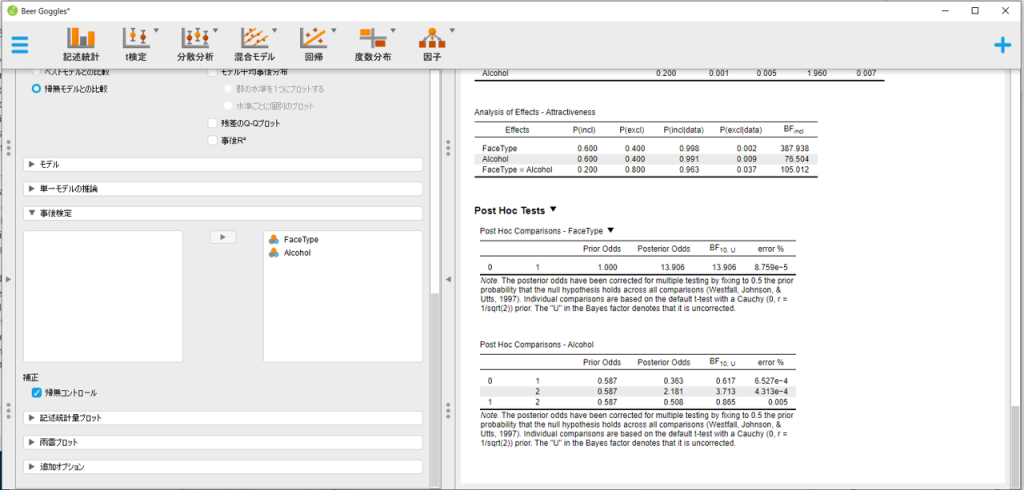
事後検定は画面左の”事後検定”のメニューから行います。単純主効果の検定に相当する出力がありませんが,おそらくまだ議論中の部分なので実装されていないのだと思われます。素朴には比較したい水準同士をベイジアンt検定にかければよく,Wastfall(1997)の補正法なども提案されています(Bergh et al., 2020)。
分散分析は,実験心理学をはじめとする多くの心理学の領域において非常に馴染み深い分析です。心理統計を取り巻く環境は日々変わりつつありますが,今後急速に分散分析が使われなくなる,といった状況にはならないのではないかと,個人的には思います。ベイジアンANOVAを行える統計ソフトとして,JASPは非常に取っつきやすく,お勧めできるソフトです。
(記事が長くなってしまったので,共分散分析の説明は次回に回したいと思います)
van den Bergh, D., van Doorn, J., Marsman, M., Draws, T., van Kesteren, E., Derks, K .. & Wagenmakers, E. (2020). A Tutorial on Conducting and Interpreting a Bayesian ANOVA in JASP. L’Année psychologique, 120, 73-96. https://doi.org/10.3917/anpsy1.201.0073
Kass, R. E., & Raftery, A. E. (1995). Bayes factors. Journal of the american statistical association, 90(430), 773-795.
Westfall, P. H. (1997). Multiple testing of general contrasts using logical constraints and correlations. Journal of the American Statistical Association, 92 (437), 299{306.