この記事は Stan Advent Calendar 2020 の8日目の記事になります。本日は,信号検出理論について解説していきます。
1. 信号検出理論とは
信号検出理論(Signal Detection Theory; SDT)は古典的な認知モデルの1つです。急に”認知モデル”という言葉が出てきましたが,認知モデルとは,知覚や学習や記憶といった人間の認知過程を説明することを目的としたモデルのことです。そういった意味で,昨日までのアドベントカレンダーで登場した,回帰分析やt検定,項目反応理論といった統計モデルとは,やや趣が異なります。
信号検出理論は,「無視すべき背景刺激(ノイズ)から,検出すべき刺激(信号)を見つける」ような状況に適用することができます。例えば聴覚検査では,検査の参加者は何らかの音(信号)が鳴ったらボタンを押して反応することを求められますし,記憶の実験では,呈示された単語について,すでに学習した単語(信号)か学習していない単語(ノイズ)かを問う,再認課題と呼ばれる手続きが用いられることがあります。参加者の反応は,基本的にはボタンを押す/押さない,学習した/していない,といった2値になります。
このとき,信号検出理論では,以下のようなモデルを用いて参加者の反応過程を説明します。
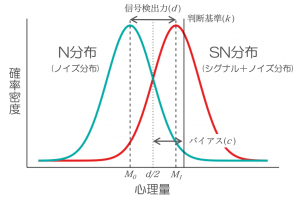
N分布はノイズが呈示された際の心理量の分布,SN分布は信号が呈示された際の心理量の分布です。心理量とはなんぞや,という感じですが,これは参加者がYes/Noの判断を行うときに参照する,何らかの心理的な量です。例えば,先ほど紹介した再認課題では,参加者は呈示された単語について,自分の中にある”単語を学習したかどうかの感覚”を頼りに判断を行い,感覚が十分に大きければYesと反応することになります。このときの”単語を学習したかどうかの感覚”が心理量に相当します。また,参加者のYes/Noの判断を分ける基準が判断基準kとなります
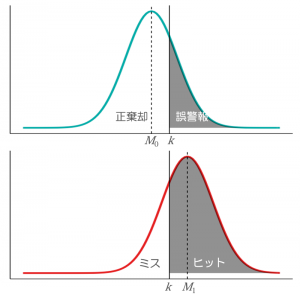
ところで,参加者は必ずしも正確にYes/Noの判断を行えるわけではありません。誤ってノイズに対してYesという反応をしてしまったり,信号に対してNoという反応をすることもあるでしょう。したがって,2値判断のデータは,呈示された刺激が信号なのかノイズなのか,それらに対する参加者の反応がYesなのかNoなのかに応じて,以下の4通りに分類することができます。
| 刺激/参加者の反応 | Yes | NO |
|---|---|---|
| 信号 | ヒット | ミス |
| ノイズ | 誤警報(FA) | 正棄却(CR) |
特に,ノイズに対するYes反応は誤警報(False Alarm; FA),ノイズに対するNo反応は正棄却(Correct Rejection; CR)と呼ばれます。図で表すと以下のようになります。
N分布の平均(M0)とSN分布の平均(M1)との距離を,N分布の標準偏差sで割った値が,信号検出力dとして定義されます。2つの分布の距離が離れるほど(dが大きくなるほど)ノイズと信号は弁別しやすくなり,反対に距離が縮まるほど弁別しにくくなります。
\(d=\frac{M_{1}-M_{0}}{s}\)
また,判断基準kとd/2の差は反応バイアスcとして定義されます。d/2はN分布とSN分布がちょうど交わる点であり,もし判断基準kとd/2が等しければ,c=0となり,反応バイアスがない状態を表します。c<0ならYes反応をしがちな,c>0ならNo反応をしがちな参加者ということになります。
\(c=k-\frac{d}{2}\)
2. Stanによる信号検出モデルの推定
それでは,Stanを使って信号検出モデルのパラメータを推定する方法について説明します…などと偉そうなことを言いましたが,実は信号検出モデルのStanへの実装は,すでに複数の書籍(Lee & Wagenmakers, 2013; 豊田, 2017)で解説されています。後者の『実践ベイズモデリング ―解析技法と認知モデル―』では,サンプルコードまで配布されていますので,これを利用しない手はありません。ダウンロードして,Rのワーキングディレクトリに入れておきましょう。
サンプルデータとして,metaSDTregパッケージに内包されている”simMetaData”というサンプルデータを使用します。25名の参加者に対して,1000試行(信号あり500試行:信号なし500試行)の2値判断課題を実施したデータです。
#パッケージ読み込み library(rstan) library(brms) library(tidyverse) library(bayesplot) library(metaSDTreg)
#データ読み込みと整形 > dat <- (metaSDTreg::simMetaData) > head(dat) id m S resp conf 1 1 1 0 0 3 2 1 2 1 1 2 3 1 3 0 1 3 4 1 4 0 1 1 5 1 5 1 1 2 6 1 6 0 0 1
“S”は刺激が信号か否か(“1″=信号),”resp”は参加者の反応(”1”=”Yes”)を表す変数です。2つの変数に基づいて反応をヒット/ミス,FA/CRの4通りに分類し,集計します。
dat <- mutate(dat,
respCode = case_when(
S==1 & resp==1 ~ "hit",
S==1 & resp==0 ~ "miss",
S==0 & resp==1 ~ "FA",
S==0 & resp==0 ~ "CR"))
SDT_dat <- list(h=length(grep("hit", dat$respCode)),
f=length(grep("FA", dat$respCode)),
MI=length(grep("miss", dat$respCode)),
CR=length(grep("CR", dat$respCode)))
ここで,ヒットの度数をh,FAの度数をfとし,信号ありの試行数をnS,信号なしの試行数をnNとします。SN分布におけるヒット率をθ(h)とすると,ヒット数hは確率θ(h),試行数nSの二項分布に従うと見なすことができます。FA数fについても同様に,確率θ(f),試行数nNの二項分布に従うと見なします。
\(h \sim \text {Binomial}\left(\theta^{(h)}, n_{S}\right)\)
\(f \sim \text {Binomial }\left(\theta^{(f)}, n_{N}\right)\)
また,ヒット率θ(h)およびFA率θ(f)は,信号検出力dと反応バイアスcの関数として,以下のように表せます。
\(\theta^{(h)}=\Phi\left(\frac{1}{2} d-c\right)\)
\(\theta^{(f)}=\Phi\left(-\frac{1}{2} d-c\right)\)
以下は,豊田(2017)の”code33_1.stan”のtransformed parametersブロックとmodelブロックの引用です。上述の通りのモデルが設定されています。
transformed parameters {
real<lower=0,upper=1> thetah;
real<lower=0,upper=1> thetaf;
thetah = Phi(d / 2 - c);
thetaf = Phi(-d / 2 - c);
}
model {
d ~ normal(0, sqrt(2));
c ~ normal(0, inv_sqrt(2));
h ~ binomial(s, thetah);
f ~ binomial(n, thetaf);
}
先ほどのデータに当てはめてみましょう。
#非階層モデル
fit_SDT <- stan(file="code33_1.stan",
data=SDT_dat,
pars=c("thetah", "thetaf", "d", "c"),
verbose=F,
seed=1969,
chains=4,
warmup=5000,
iter=10000)
> print(fit_SDT, c("thetah", "thetaf", "d", "c"))
Inference for Stan model: code33_1.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
thetah 0.84 0 0.00 0.84 0.84 0.84 0.84 0.85 12986 1
thetaf 0.49 0 0.00 0.49 0.49 0.49 0.50 0.50 18707 1
d 1.01 0 0.02 0.98 1.00 1.01 1.03 1.05 15006 1
c -0.49 0 0.01 -0.51 -0.50 -0.49 -0.49 -0.48 14590 1
ヒット率θ(h),FA率θ(f),信号検出力d,反応バイアスcといったパラメータが推定されました。ヒット率は.84とそこそこ高い値ですが,FA率も.49と高いですね。反応バイアスcが負の値であることからも,参加者は全体的にYes反応をしがちであったことが伺えます。
この分析では参加者全員分の反応データをまとめてしまっているので,これ以上の情報は得られません。次の分析では,階層モデルを使って参加者ごとにそれぞれのパラメータを推定してみましょう。
3. 階層的信号検出モデル
信号検出モデルを階層モデルに拡張します。参加者ごとに信号検出力dと反応バイアスcを求めるため,dとcの事前分布である正規分布の平均値μと標準偏差σをハイパーパラメータとして推定します。
\(d_{i} \sim \text {Normal}\left(\mu_{d}, \sigma_{d}\right)\)
\(c_{i} \sim \text {Normal}\left(\mu_{c}, \sigma_{c}\right)\)
データの方も,階層モデルにあわせて,参加者ごとの反応数が分かる形に集計し直します。ちょっとだけR力(りょく)が試されますね。
#参加者ごとに集計
grouped_dat <- dat %>%
group_by(id, respCode) %>%
tally %>%
spread(respCode, n)
hSDT_dat <- list(k=25,
h=grouped_dat$hit,
f=grouped_dat$FA,
s=500,
n=500)
kは参加者数,sは信号あり試行数,nは信号なし試行数を表します。豊田(2017)の”code33_2.stan”を使って,階層的信号検出モデルを当てはめてみましょう。
#階層モデル
fit_hSDT <- stan(file="code33_2.stan",
data=hSDT_dat,
pars=c("thetah", "thetaf", "d", "c", "mud", "muc", "sigmad", "sigmac"),
verbose=F,
seed=1969,
chains=4,
warmup=5000,
iter=10000)
print()関数で結果が出力されます。先ほどの非階層モデルとは異なり,各パラメータが参加者ごとに推定されているのが分かるかと思います。
print(fit_hSDT, pars=c("thetah", "thetaf", "d", "c", "mud", "muc", "sigmad", "sigmac"))
出力が多いのでここでは割愛しますが,代わりに信号検出力dと反応バイアスcを参加者ごとに図示してみましょう。bayesplotパッケージのmcmc_intervals_data()関数を使って推定結果を取り出し,ggplot()関数を使って点推定値(中央値)の昇順に並べ替えて図示しています(なお,bayesplotパッケージの日本語解説はStan Advent Calendar2018の2日目と8日目の記事に詳しいです)。
#dとcを参加者ごとに図示 sample_hSDT <- as.array(fit_hSDT) hSDT_d <- mcmc_intervals_data(sample_hSDT, regex_pars="d\\[", prob=0.95, prob_outer=T) ggplot(hSDT_d, aes(x = m, y = reorder(parameter, m))) + geom_errorbar(aes(xmin = ll, xmax = hh), width = 0.5) + geom_point(shape = 15, size = 4) + labs(x = "d", y = "ID") hSDT_c <- mcmc_intervals_data(sample_hSDT, regex_pars="c\\[", prob=0.95, prob_outer=T) ggplot(hSDT_c, aes(x = m, y = reorder(parameter, m))) + geom_errorbar(aes(xmin = ll, xmax = hh), width = 0.5) + geom_point(shape = 15, size = 4) + labs(x = "c", y = "ID")
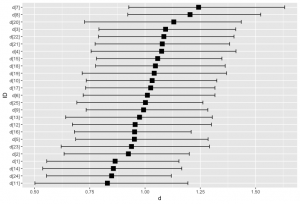
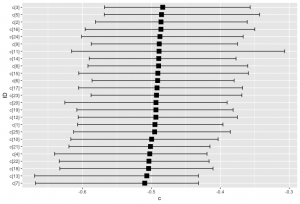
dについては多少バラつきがありますが,cについては参加者間でほとんどバラついておらず,一貫してYes反応へのバイアスがかかっていることが伺えます。階層モデルで参加者ごとにパラメータを推定することで,別途測定した参加者の特性と,信号検出モデルのパラメータの関連を見る,といった使い方も可能になるでしょう。
4. まとめ
以上,信号検出理論の概要と,Stanによる信号検出モデルの実装方法についてご説明してきました。信号検出モデルは仮定がシンプルなだけに,色々な事態に適用可能な汎用的なモデルだと思います。また,不等分散信号検出モデル(Jang et al., 2009)や二次元信号検出モデル(Soto et al., 2017),タイプ2信号検出モデルといった様々な発展的モデルも存在しています。「最近モデリングって言葉をよく聞くけど,なんか難しそう…」と感じておられる方は,信号検出モデルのようなシンプルなモデルをベースとして,自分の研究にフィットするモデルに徐々に修正していく,というアプローチもアリかもしれません。
Enjoy!
Reference
- Jang, Y., Wixted, J. T., & Huber, D. E. (2009). Testing signal-detection models of yes/no and two-alternative forced-choice recognition memory. Journal of Experimental Psychology: General, 138(2), 291-306.
- Lee, M. D., & Wagenmakers, E. J. (2013). Bayesian cognitive modeling: a practical course. Cambridge, UK: Cam- bridge University press. 井関龍太(訳)・岡田謙介
(解説)(2017)ベイズ統計で実践モデリング:認知モデルのトレーニング 北大路書房. - Maniscalco, B., & Lau, H. C. (2014). Signal detection theory analysis of Type 1 and Type 2 data: Meta-d’, response-specific Meta-d’, and the unequal variance SDT model. In: Fleming, S. M., Frith, C. D. (Eds), The Cognitive Neuroscience of Metacognition. Berlin Heidelberg: Springer, 2014.
- Soto, F. A., Zheng, E., Fonseca, J., & Ashby, F. G. (2017). Testing separability and independence of perceptual dimensions with general recognition theory: A tutorial and new R package (grtools). Frontiers in psychology, 8, 696.
- 豊田秀樹(編)(2017)実践ベイズモデリング:解析技法と認知モデル 朝倉書店.